نعرف في المقالة لغزا جديدا من أبرز اسرار وخفايا وهو سر الرقم 42 وسنحاول في تلك المقالة محاولة حل لغز الرقم 42 فتابعوا المقالة لمعرفة كل ذلك.
مقدمة حول سر الرقم 42
الجميع مفتون بالقضايا التي لم يتم حلها ، مثل وفاة الوزير روبرت بولين أو اختفاء كزافييه دوبون دي ليغونيه. يظل هذا صحيحًا حتى لو كانت هناك في الأصل مزحة واحدة ،
كما هو الحال في رواية الخيال العلمي The Hitchhiker’s Guide to the Galaxy ، والتي ظهرت باللغة الإنجليزية عام 1979.
يذكر مؤلفها دوجلاس آدامز في الجزء الأخير من هذا العمل أن الإجابة على السؤال الكبير حول الحياة والكون وكل شيء هو 42 ( “الإجابة على السؤال النهائي للحياة والكون وكل شيء هي 42” ).
تدور هذه الرواية الأولى في سلسلة من خمس روايات حول جهاز كمبيوتر فائق القوة والذي ، بينما يحوسبه أكثر من 7.5 مليون سنة ، ينتهي به الأمر بالإجابة على “42” لأولئك الذين يسألونه عن السؤال النهائي حول الحياة والكون وكل شيء بينهما.
أدركت الشخصيات ، للأسف ، أن الإجابة المقدمة في نهاية القصة الأولى ليست مفيدة للغاية ، حيث لم تتم صياغة السؤال بوضوح ودقة كافية.
ثم يجيب الكمبيوتر أنه للعثور على الصياغة الصحيحة للسؤال ، والإجابة عليه هي 42 ، سيتعين عليه إنشاء نسخة جديدة من نفسه وسيستغرق ذلك وقتًا.
ما هو سر الرقم 42
سر الرقم 42 هو عنصر أساسي في ثقافة المهوس وهو مصدر عدد كبير من النكات والغمزات المتبادلة بين المطلعين. على سبيل المثال ، إذا سألت محرك البحث الخاص بك عن الإجابة على ” السؤال الكبير حول الحياة والكون والبقية ” ، فمن المرجح أن يجيب: ” 42 “.
هذا هو الحال على سبيل المثال بالنسبة لـ Google ، و Qwant ، و Wolfram Alpha ، المتخصص في مسائل الحساب الرياضي ، ولكن أيضًا بالنسبة لمساعد حوار Cleverbot.
تم إنشاء مدارس الكمبيوتر الخاصة المعروفة باسم “42 مدرسة” في عام 2013 وتم اختيار اسمها بوضوح في إشارة إلى روايات دوغلاس آدامز. تم التخطيط لتطوير “الحرم الجامعي 42” الجديد في الخارج بمعدل عشرة سنويًا.
يظهر الرقم 42 أيضًا بأشكال مختلفة في فيلم Spider-Man: New Generation.
ستجد عددًا كبيرًا من الأحداث المتعمدة الأخرى والإشارات إلى 42 مدرجة ، على سبيل المثال في مقالة ويكيبيديا “السؤال الكبير عن الحياة والكون والبقية” .
الأكثر غرابة ، ولكن هذه المرة كانت مصادفة من غير المجدي البحث عن معانيها ، فقد لوحظ ، من بين أشياء أخرى كثيرة ، حيث تشمل أسرار الرقم 42 ما يلي:
- في مصر القديمة ، أثناء حكم الروح ، كان على الميت أن يعلن أمام 42 قاضيًا أنه لم يرتكب 42 خطايا [انظر مقال ويكيبيديا “دينونة الروح (مصر القديمة)”] ؛
- المسافة التي يجب قطعها في سباق الماراثون هي 42.195 كيلومترًا لأن هذه هي المسافة التي قطعها الرسول اليوناني فيليبيدس في عام 490 قبل الميلاد بين ماراثون وأثينا ليعلن النصر على الفرس. إن حقيقة عدم تحديد الكيلومتر في ذلك الوقت ينبغي أن تزيد من دهشتنا ؛
- كان هناك 42 إمبراطورًا تبتيًا قديمًا. نياتري تسينبو ، الذي حكم حوالي 127 قبل الميلاد ، كان الأول ، ولانغدارما ، الذي حكم من 836 إلى 842 ، كان الأخير (انظر مقالة ويكيبيديا “قائمة أباطرة التبت”) ؛
- كتاب جوتنبرج للكتاب المقدس ، وهو أول كتاب طُبع في أوروبا ، يحتوي على 42 سطراً من النص لكل عمود ويسمى أيضًا “الكتاب المقدس اللاتيني المكون من اثنين وأربعين سطراً” ؛
سُئل بالطبع عما إذا كان استخدام العدد 42 في رواية دوجلاس آدامز له أي معنى خاص في ذهنه. جوابه واضح: كانت مزحة. كان يجب أن يكون عددًا عاديًا وصغيرًا نوعًا ما ، واخترت هذا الرقم.
التمثيلات الثنائية ، القاعدة 13 ، رهبان التبت مجرد هراء. جلست إلى مكتبي ، ونظرت في الفناء الخلفي ، وفكرت أن “42 ستذهب” وكتبتها ” .
يأتي استحضار القاعدة 2 مما هو مكتوب في 42 في النظام الثنائي 101010 ، وهو أمر بسيط للغاية وقد أدى أيضًا إلى إقامة حفلة لبعض المهووسين في 10 أكتوبر 2010 (10-10-10) . يمكن تفسير ذكر الأساس 13 في إجابته بطريقة غير مباشرة.
ذكرت الرواية في عدة مناسبات أن 42 سيكون الجواب على السؤال “كم يساوي 6 ضرب 9؟”. بالطبع ، هذا سخيف ، لأن 6 × 9 = 54 … ولكن على وجه التحديد ، في الأساس 13 ، الرقم المكتوب 42 يساوي 4 × 13 + 2 = 54 .
بجانب الأحداث التي قدمها علماء الكمبيوتر طواعية للمتعة ، واللقاءات الحتمية مع الرقم 42 عندما ننظر في كل مكان في التاريخ أو في العالم ، لا يزال بإمكاننا التساؤل عما إذا كان الرقم 42 هو رقم معين من وجهة النظر الصارمة للرياضيات.
الرقم 42 رياضيا؟
فيما يلي قائمة ببعض الخصائص الرياضية لـ 42.
- 42 هو مجموع القوى الثلاث الأولى لأسين فرديين (2¹ + 2³ + 2⁵ = 42) . التسلسل a (n) لمجموع القوى الفردية لـ 2 هو التسلسل A020988 من موسوعة Neil Sloane للتسلسلات الرقمية ( https://oeis.org ).
في الأساس 2 ، يتم كتابة العنصر n من الرقم 1010 … 10 ، مع تكرار “10” n مرة ، وصيغته هي a (n) = (2/3) (4 ⁿ – 1 ). مع زيادة n ، يتجه تكرار هذه الأرقام نحو الصفر ، مما يعني أن الأرقام التي تنتمي إلى هذه القائمة ، وبالتالي 42 نفسها ، نادرة بشكل استثنائي.
- 42 هو مجموع الأسس الأولين للعدد 6 مع الأس غير الصفري (6¹ + 6² = 42) . التسلسل ب (ن) لمجموع قوى العدد 6 هو التسلسل A105281 من موسوعة سلون. يتم تعريفه بواسطة الصيغ b (0) = 0 ، b (n) = 6b (n – 1) +6 . تردد هذه الأرقام يميل أيضًا من 0 إلى ما لا نهاية.
- 42 رقم كتالوني. تم ذكر الأرقام الكاتالونية ، تحت اسم آخر ، لأول مرة من قبل ليونارد أويلر ، الذي أراد معرفة عدد الطرق المختلفة لتقطيع عدة مثلثات مضلع محدب مع n جوانب من خلال ربط الرؤوس بمقاطع خطية.
بداية التسلسل (A000108 في Neil Sloane) هي 1 ، 1 ، 2 ، 5 ، 14 ، 42 ، 132 ، … الصيغة c (n) = (2n)! / (N! (N + 1)!) يعطي الحد من رقم n من هذا التسلسل من الأرقام التي كثافتها ، مثل تلك التي تسبقها ، تساوي صفرًا عند اللانهاية.
- تمت تسمية الأرقام الموجودة في تسلسل c (n) تكريماً لعالم الرياضيات الفرنسي البلجيكي يوجين تشارلز كاتالان (1814-1894) ، الذي اكتشف أن c (n) هو عدد الطرق لترتيب n أزواج من الأقواس مع احترام المعتاد. قواعد كتابة الأقواس: لا يتم إغلاق الأقواس أبدًا قبل أن يتم فتحها ، ولا يمكن إغلاق الأقواس إلا عندما يتم إغلاق كل تلك التي تم فتحها منذ فتحها.
على سبيل المثال ، ج (3) = 5 لأن الترتيبات الممكنة لثلاثة أزواج من الأقواس هي: ((())) ؛ () () () ؛ (()) () ؛ (() ()) ؛ () (()).
- الرقم c (n) هو أيضًا عدد الأشجار الثنائية التي تحمل أوراق n + 1. وهو أيضًا عدد المسارات الصاعدة على شبكة تقع أسفل القطر الأول.
هذه الخاصية تجعل من الممكن فهم التعريف عن طريق استقراء شروط التسلسل الكتالوني ، c (0) = 1 و c (n + 1) = Σ c (k) c (n – k) ، المجموع المتعلق بـ تتراوح ك من 0 إلى ن .
في الواقع ، لحساب عدد المسارات التي تصل إلى الحد الأقصى n + 1 ، فإننا نعتبر نقطة وسيطة ، منخفضة قدر الإمكان ، تلامس القطر ؛ أولئك الذين قبل (أسفل القطر تمامًا) أعطوا c (n – k) ، أولئك الذين بعدهم (أدناه بالمعنى الواسع للقطر) أعطواج (ك) .
سر الرقم 42 في عدد كاتالان
نادرة للغاية ، أكثر بكثير من الأعداد الأولية: أربعة عشر فقط من هذه الأرقام أقل
من 1 مليار. تتمة لهم يبدأ:
1، 1، 2، 5، 14، 42، 132، 429، 1،430، 4،862، 16796، 58،786، 208،012، 742،900، 2674،440، 9،694،845، 35،357،670، 129،644،790، 477638700، 1767263190، 6564 120440، 24466267020 ، 91482563640 ، 343059613650 ، 1289904147324 ، 4861946401452 ، 18367353072152 ، 69533550916004 ، 263747951750360 ، …
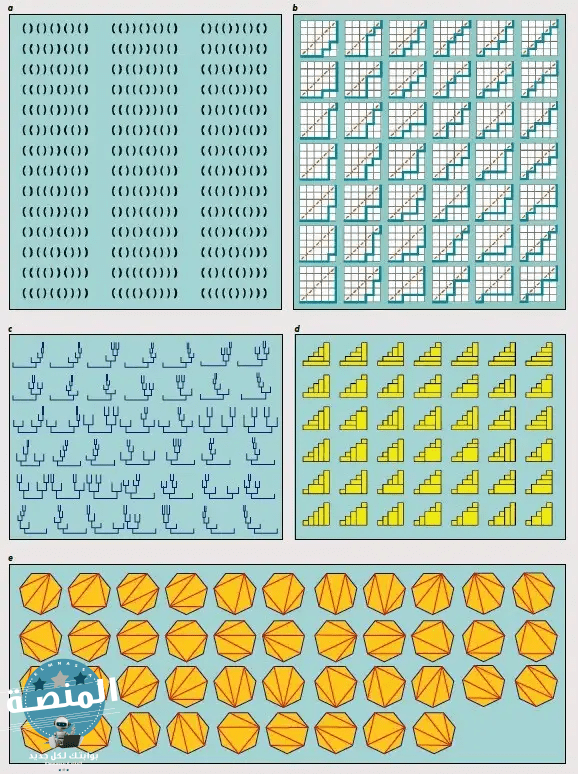
الرقم 42 هو الرقم الكتالوني c (5) . على وجه الخصوص ، هذا يعني أن هناك 42 طريقة لوضع 5 أزواج من الأقواس بشكل صحيح (أ) : لا يُغلق الزوج أبدًا حتى يتم فتحه ، ولا يغلق أبدًا قبل كل تلك المفتوحة منذ فتحه. تم فتح نفسها مغلقة.
هذا يعني أيضًا أننا إذا أعطينا أنفسنا شبكة من الضلع 5 وأننا ، باتباع جوانب مربعات رقعة الداما ، نريد ربط الزاوية اليسرى السفلية بالركن الأيمن العلوي دون قطع القطر وبدون النزول مطلقًا تكرارا. ، هناك 42 طريقة للقيام بذلك (ب) .
وبالمثل ، فإن عدد الأشجار الثنائية المكونة من 6 أوراق هو 42 (ج) ، وعدد الطرق لتمهيد جانب سلم مكون من 5 خطوات مع مستطيلات هو 42 (د) ، وعدد الطرق لقطع سباعي منتظم في عدة مثلثات من خلال ضم الرؤوس هو 42 (هـ) .
42 هو رقم “عملي” ، مما يعني أن أي عدد صحيح بين 1 ونفسه هو مجموع بعض مقسوماته (المميزة).
الأرقام العملية الأولى هي 1 ، 2 ، 4 ، 6 ، 8 ، 12 ، 16 ، 18 ، 20 ، 24 ، 28 ، 30 ، 32 ، 36 ، 40 ، 42 ، 48 ، 54 ، 56 ، 60 ، 64 ، 66 ، 72 (استمرار A005153 بواسطة نيل سلون).
لا نعرف أي صيغة بسيطة تعطي الحد من رقم n من هذه المتتالية ، ويبدو التكرار المحدود لشروطها موجبًا هذه المرة.
كل هذا ممتع ، لكن من الخطأ القول إن 42 رائعة حقًا في الرياضيات. الأرقام 41 أو 43 ، على سبيل المثال ، تنتمي أيضًا إلى العديد من السلاسل.
تمت دراسة مشكلة معرفة الأرقام الأكثر إثارة للاهتمام بشكل خاص أو غير المثير للاهتمام بشكل خاص ، بدءًا من الأجنحة التي سردها نيل سلون في موسوعته.
إلى جانب الارتباط النظري بتعقيد Kolmogorov (الأرقام المثيرة للاهتمام هي تلك التي تحتوي على وصف موجز على الأقل) ، فقد ظهر تأثير ثقافي محدد للأرقام التي احتفظت بها موسوعة Neil Sloane ، وهو بالتالي شيء آخر.
من موسوعة قائمة على الموضوعية الرياضية البحتة (انظر الببليوغرافيا).
من الرقم 42 إلى مشكلة مجاميع المكعبات الثلاثة!
يعرف علماء الكمبيوتر وعلماء الرياضيات جاذبية الرقم 42 وقد اعتقدوا دائمًا أنها كانت لعبة بسيطة يمكن لعبها بسهولة برقم آخر. لا يزال هناك خبر حديث جعلهم مستمتعين. العدد 42 في الواقع تسبب في مشاكل أكثر بكثير من أي رقم آخر أقل من 100 في مسألة 3 مكعبات .
تم تحديد مشكلة المكعبات الثلاثة على النحو التالي:
ما هي الأعداد الصحيحة ن التي يمكن كتابتها كمجموع ثلاثة مكعبات من الأعداد الصحيحة ، ن = أ ³ + ب ³ + ج ؟ وعندما يحدث ذلك ، كيف تجد أ ، ب ، ج؟
تنشأ الصعوبة ، حتى على المستوى العملي في إجراء العمليات الحسابية ، من حقيقة أن مساحة الثلاثية التي سيتم استكشافها تتضمن أعدادًا صحيحة سالبة بالنسبة إلى n معطى.
وبالتالي فإن هذه المساحة غير محدودة ، وهذا ليس هو الحال عندما نهتم بمجموع المربعات: في مثل هذا المجموع من المربعات يعطي n ، يكون لكل مربع قيمة مطلقة أقل من n . علاوة على ذلك ، بالنسبة لمجموع المربعات ، نعلم جيدًا ما هو ممكن ومستحيل.
الرقم 42 في مجاميع المربعات
نحن نعلم فقط منذ سبتمبر 2019 أن العدد 42 هو مجموع ثلاثة مكعبات. يصعب إتقان مجاميع المكعبات بسبب الأعداد الصحيحة السالبة. في المقابل ، فإن مجاميع
الأعداد الصحيحة المربعة ، التي اهتم بها علماء الرياضيات منذ العصور القديمة ، أصبحت معروفة الآن. ها هي نتائجهم.
الرقم 42 في مجموع مربعين
– العدد الأولي الفردي هو مجموع مربعين من الأعداد الصحيحة فقط إذا كان بالشكل 4k + 1 . ثم يكون تحلل مجموع مربعين فريدًا. أمثلة: 5 = 1² + 2² ، 13 = 2² + 3² ، 17 = 1² + 4² .
– العدد الصحيح n هو مجموع مربعين إذا وفقط إذا حدث كل عامل من عوامله الأولية بالشكل 4k + 3 مع أس زوجي في التحليل الأولي لـ n .
مثال: 45 = 3²5 = 6² + 3².
التحليل الأولي لـ 45 يتضمن 3 ، وهي على شكل 4k + 3 ، مع أس زوجي. العدد 45 ، بالتالي ، يفي بشرط النظرية ويتم كتابته بشكل فعال كمجموع مربعين
(انظر نظرية فيرما ذات المربعين).
الرقم 42 في مجموع ثلاثة مربعات
– جميع الأعداد الصحيحة باستثناء تلك التي على شكل 3n و 8n + 7 هي مجاميع من ثلاثة مربعات
(انظر نظرية ثلاثة مربعات).
الرقم 42 في مجموع أربعة مربعات
أي عدد صحيح هو مجموع أربعة مربعات. تم توضيح هذه النظرية الرائعة في عام 1770 من قبل لاجرانج وتم عرضها مرة أخرى في عام 1772 بواسطة أويلر.
(انظر نظرية المربعات الأربعة لاجرانج).
في حالة المكعبات ، نجد حلولًا كبيرة جدًا غير متوقعة ، مثل حل 156 ، الذي تم اكتشافه في عام 2007:
156 = 26577110807569³ + (- 18161093358005) ³ + (- 23381515025762) ³ .
أول شيء يجب ملاحظته لأي شخص مهتم بمجموع ثلاثة مكعبات هو أنه بالنسبة لبعض قيم العدد الصحيح n ، لا يوجد حل للمعادلة n = a³ + b³ + c³ .
هذا هو الحال بالنسبة لجميع الأعداد الصحيحة n بالشكل 9 م + 4 و 9 م + 5 (على سبيل المثال 4 ، 5 ، 13 ، 14 ، 22 ، 23 ).
الدليل على هذا البيان بسيط للغاية. نحن نستخدم حساب ” modulo 9 ” ، والذي يرقى إلى افتراض أن 9 = 0 ومعالجة الأرقام فقط بين 0 و 8 أو بين – 4 و + 4 .
نلاحظ أولاً أن:
- 0³ = 0 (طراز 9) ؛
- 1³ = 1 (طراز 9) ؛
- 2³ = 8 = – 1 (طراز 9) ؛
- 3³ = 27 = 0 (طراز 9) ؛
- 4³ = 64 = 1 (طراز 9) ؛
- 5³ = (- 4) ³ = – 64 = – 1 (نموذج 9) ؛
- 6³ = (-3) ³ = 0 (نموذج 9) ؛
- 7³ = (- 2) ³ = 1 (نموذج 9) ؛
- 8³ = (- 1) ³ = –1 (نموذج 9).
بعبارة أخرى: modulo 9 ، مكعب عدد صحيح يستحق إما – 1 (= 8) ، أو 0 ، أو 1 . ومع ذلك ، فإن إضافة ثلاثة أرقام مختارة من 0 و 1 و – 1 تعطي:
- 0 = 0 + 0 + 0 = 0 + 1 + (- 1) ؛
- 1 = 1 + 0 + 0 = 1 + 1 + (- 1) ؛
- 2 = 1 + 1 + 0 ؛ 3 = 1 + 1 + 1 ؛
- 6 = – 3 = (- 1) + (- 1) + (- 1) ؛
- 7 = – 2 = (- 1) + (- 1) + 0 ؛
- 8 = – 1 = (- 1) + 0 + 0 = 1 + (- 1) + (- 1).
لا نحصل أبدًا على 4 أو 5 (= – 4) . هذا يعني أن مجاميع المكعبات الثلاثة ليست أبدًا أرقامًا بالصيغة 9 م + 4 أو 9 م + 5 . سنقول أن n = 9m + 4 و n = 9m + 5 هي قيم ممنوعة.
البحث عن الحلول عمليا في حل لغز الرقم 42
لتوضيح مدى صعوبة البحث عن حلول للمعادلة n = a³ + b³ + c³ ، دعنا نوضح ما يحدث لـ n = 1 و n = 2 .
بالنسبة إلى n = 1 ، يوجد الحل الواضح 1³ + 1³ + (- 1) ³ = 1 .
هل هناك آخرون؟ نعم :
9³ + (- 6) + (- 8) ³ = 729 + (- 216) + (- 512) = 1 .
ليس هذا هو الحل الوحيد ، لأنه في عام 1936 ، اقترح عالم الرياضيات الألماني كورت مالر حلولًا لا نهاية لها. لجميع الأعداد الصحيحة p:
(9p⁴) ³ + (3p – 9p⁴) ³ + (1–9p³) ³ = 1.
لقد أثبتنا النتيجة باستخدام الهوية الرائعة:
(A + B) ³ = A³ + 3A²B + 3 AB² + B³.
مجموعة الحلول اللانهائية معروفة أيضًا بـ n = 2 ؛ تم اكتشافه في عام 1908 من قبل AS Werebrusov. لجميع الأعداد الصحيحة p:
(6p³ + 1) ³ + (1–6p³) ³ + (- 6p2) ³ = 2 .
بضرب كل حد من هذه المساواة في مكعب عدد صحيح ، r³ ، نستنتج أن هناك أيضًا عددًا لانهائيًا من الحلول لأي مكعب لعدد صحيح وأي مضاعف لمكعب عدد صحيح.
على سبيل المثال 16 ، وهو ضعف مكعب 2 ، لدينا: 14³ + (- 10) ³ + (- 12) ³ = 16
دعنا نشير أيضًا إلى أنه بالنسبة لـ n = 3 ، في أغسطس 2019 ، كان هناك حلان فقط معروفان:
1³ + 1³ + 1³ = 3 و 4³ + 4³ + (- 5) ³ = 3 .
ثم يتبادر إلى الذهن السؤال بشكل طبيعي: هل توجد حلول لجميع القيم غير المحظورة لـ n ؟
وبذلك فقد عرفنا لغز الرقم 42 و لمعرفة سر سر رقم 369 أو ما يسمي كود تردد 369 تسلا يمكنك الاطلاع عليه من هنا